| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- BFS
- SinglyLinkedList
- array
- VCS
- stack
- 자료구조
- Java
- Union Find
- Bellman-Ford
- Easy
- Medium
- heap
- String
- hash
- LinkedList
- Hashtable
- leetcode
- A* Algorithm
- ArrayList vs LinkedList
- 구현
- sorting
- graph
- Leedcode
- hash table
- greedy
- Two Pointers
- python3
- DailyLeetCoding
- dfs
- 광연자동차운전면허학원
- Today
- Total
Min IT's Devlog
[python3] 785. Is Graph Bipartite? 본문
풀이 일자: 23.05.19
난이도: [Medium]
분류: [DFS, BFS, Union Find, Graph]

문제 내용
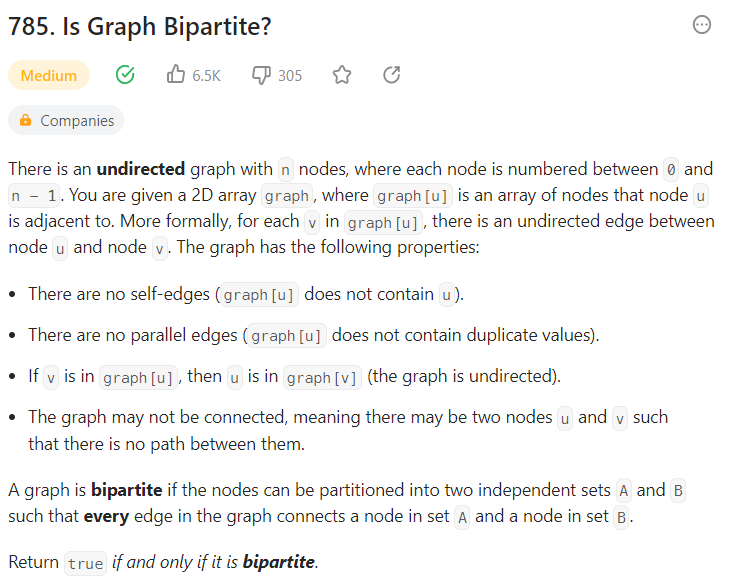
이번 문제는 undirected graph가 주어졌을 때 이 노드들을 A와 B그룹으로 나눌 수 있는지 여부를 리턴하는 문제로 각 A,B 내부의 노드끼리는 연결되어 있지 않아야 한다. A와 B는 연결되어 있어도 상관없다.
문제 해결 흐름
1. 처음에는 Graph문제이고 A와 B그룹으로 나눌 수 있기 때문에 Union-Find를 떠올렸다.
→ 가능은 하겠지만 좀더 쉬운 방법을 떠올리고자 했다
2. A그룹과 B그룹을 나누고 같은 그룹의 노드들이 서로 인접하면 안되기 때문에 노드를 색칠하는 문제로 생각해도 되겠다는 생각을 할 수 있다.
→ BFS를 이용하여 각 level별로 같은 색으로 색칠하다가 만약 인접 노드에 같은 색을 칠한 노드가 있다면 False를 리턴한다.
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
n = len(graph)
visited = [-1 for _ in range(n)];
for i in range(n): # 노드 전체를 순회
if visited[i] == -1: # 방문한 적이 없다면
q = deque();
visited[i] = 0; # 해당노드를 방문했다고 보고
q.appendleft([i,0]); # 해당 노드를 넣음
while q:
n, color = q.pop();
for j in graph[n]: # 주변에 있는 node확인
if visited[j] == -1: # 방문한 적이 없다면
nextColor = 0 if color & 1 else 1;
visited[j] = nextColor;
q.appendleft([j, nextColor]);
else: # 방문한 적이 있으면
if color^visited[j]: pass
else: return False
return True

Time Complexity: O(N^2)
반복문이 3개가 중첩되기는 하지만 독자적인 노드가 많을 수록 주변 노드에 대한 순회는 줄어들 것이고 연결되어있는 노드가 많을 수록 내부 반복문이 덜 수행될 것이기 때문에 약 N^2정도로 볼 수 있다.
Space Complexity: O(N)
visited와 q를 사용했고 여기에 들어가는 데이터가 노드의 갯수 N개가 최대이기 때문에 O(N)의 공간복잡도를 가진다고 볼 수 있다.
다른 해결 방식
1. 사실 DFS를 이용한다면 q를 사용하지 않아도 되기 때문에 공간 복잡도가 조금 줄어들 수 있다.(다른 사람 풀이)
class Solution:
def isBipartite(self, graph):
n = len(graph)
colors = [0] * n
for i in range(n): # 전체 순회를 하면서
if colors[i] == 0: # 방문하지 않았다면
if not self.dfs(graph, colors, i, 1):
return False
return True
def dfs(self, graph, colors, node, color):
if colors[node] != 0: # 0이 아니면 주변노드와 같은지 비교해서 리턴
return colors[node] == color
colors[node] = color # 0 이면 주어진 색깔을 칠함.
for neighbor in graph[node]: # 이웃을 순회
if not self.dfs(graph, colors, neighbor, -color):
return False
return True
Time Complexity: O(N^2)
이 풀이도 내 풀이와 비슷하게 N^2정도의 시간복잡도를 가질 것인데 이는 외부 for문과 dfs내부의 이웃을 순회하는 부분에서 기인한 것이다.
Space Complexity: O(N)
공간복잡도가 같은 N이긴 하지만 colors만 사용했기 때문에 내 풀이보다 실제로는 더 작은 용량을 차지할 것이다.
문제 링크
https://leetcode.com/problems/is-graph-bipartite/description/
Is Graph Bipartite? - LeetCode
Can you solve this real interview question? Is Graph Bipartite? - There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. Mo
leetcode.com
'코테 > LeetCode(Solve)' 카테고리의 다른 글
| [python3] 1396. Design Underground System (1) | 2023.05.31 |
|---|---|
| [python3] 347. Top K Frequent Elements (1) | 2023.05.22 |
| [python3] 1557. Minimum Number of Vertices to Reach All Nodes (1) | 2023.05.18 |
| [python3] 2130. Maximum Twin Sum of a Linked List (1) | 2023.05.17 |
| [python3] 24. Swap Nodes in Pairs (1) | 2023.05.16 |




