| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- DailyLeetCoding
- BFS
- Hashtable
- heap
- hash table
- dfs
- stack
- graph
- leetcode
- 구현
- String
- Union Find
- ArrayList vs LinkedList
- sorting
- hash
- Java
- LinkedList
- A* Algorithm
- 광연자동차운전면허학원
- Two Pointers
- Easy
- Medium
- SinglyLinkedList
- Bellman-Ford
- python3
- array
- 자료구조
- Leedcode
- greedy
- VCS
- Today
- Total
Min IT's Devlog
[python3] 904. Fruit Into Baskets 본문
풀이 일자: 23.02.07
난이도: [Medium]
분류: [Array, Hash Table, Sliding Window]

문제 내용
농장에서 일렬로 세워진 나무에서 과일을 따는 문제이다.
주어진 조건으로는
1) 2개의 바구니를 가지고 있고 바구니에는 각각 한 종류의 과일만 넣을 수 있고 한 바구니에 넣을 수 있는 과일 양은 무한
2) 하나의 나무에서 한 개의 과일만 딸 수 있다
3) 시작점을 자신이 정할 수 있고 시작점부터 과일을 따다가 3번째 종류의 과일이 나오는 경우 그 즉시 stop.
문제 해결 흐름
1. 간단하게 생각한다면 2중 for문을 이용해서 해결한다면 쉽겠다.
→ 바깥 for문은 시작점 내부 for문은 현재 따고 있는 위치라고 생각한다면 딴 과일의 종류를 array나 dictionary에 저장해놓고 3번째 종류의 과일이 나오면 내부 for문에서 break해서 나온다면 충분히 풀 수 있겠다. ( 모든 경우의 수를 생각해보는 방법)
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
ans = 1;
length = len(fruits);
for i in range(length - 1):
basket = [];
fruitnum = 0;
for j in range(i, length):
if len(basket) != 2:
if fruits[j] not in basket:
basket.append(fruits[j]);
else:
if fruits[j] not in basket:
break;
fruitnum += 1;
ans = max(ans, fruitnum);
if ans > (length - i - 1): // 현재의 max값과 남은 나무 값을 비교
break; // 만약 max값이 더 크면 더이상 비교할 필요X
return ans;
=> 간단한 풀이이지만 시간과 메모리 사용의 측면에서 모두 꽝인 해결책이다.
Time Complexity: O(N^3)
2중 for문은 바로 확인이 되며 배열 내부에 있는지 확인하는 not in부분도 사실상 for문이기 때문에 N^3의 Time Complexity를 가지고 있는 극악의 코드이다.
Space Complexity: O(1)
basket이라고 하는 과일의 종류를 기록하지만 해당 배열에는 최대 3개의 과일만이 들어가기에 O(1)이라고 볼 수 있다.
다른 해결 방식
1. 현재 Time Complexity가 너무 높게 나왔기 때문에 이를 줄일 수 있는 방법이 있지 않을까?
→ 탐색을 할 때 가장 빠른 것은 이진탐색이겠지만 정렬이 되어있다던가 정렬의 의미가 없기 때문에 할 수 없이 선형탐색 단 한번으로 이 문제를 처리할 수 있는 알고리즘을 생각해야겠다.
→ 어떤 범위 내의 데이터에 대한 탐색을 하는데 도움을 주는 알고리즘 Sliding Window를 약간 변형해서 사용하자
기존의 Sliding Window는 전체 배열 중 특정 범위의 데이터의 최댓값을 구하라는 문제 등에 자주 사용하는데 일정한 크기의 윈도우를 가지고 이를 움직여가며 처리하는 알고리즘이다. 이와 관련된 내용은 다음에 포스팅하겠습니다.
[과정] ( 가능한 경우의 수는 상관이 없고 오로지 최대값만 구하는 방법)
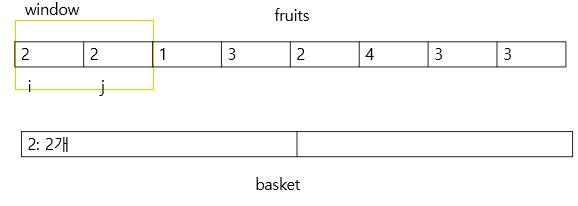
1. 아래의 fruits배열이 주어졌고 i를 window의 시작점 j를 window의 끝 점이라고 가정해보자.
( Window는 과일을 따는 범위라고 생각하면 좋다.)

2. 우선 현재 basket에는 2라는 과일만 존재한다. 2가지 종류의 과일을 딸 수 있으니까 과일을 더 딸 수 있을 것이다.
2종류의 과일을 딸 수 있을 때까지 j를 증가시킨다.
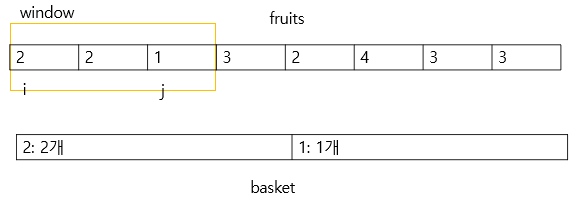
3. 다음 j를 증가시키면 3이라는 과일이 나오면서 basket에는 해당 과일을 넣을 수 없게 된다.

4. 이런 경우 이전의 최대 window의 크기였던 3을 유지하면서 window의 시작점을 1 증가시켜서 확인해본다.

5. 여전히 넣을 수 없다. 이 경우 i와 j를 같이 1씩 움직여서 가능한지 확인한다.

6. 가능한 경우 또 j만 1을 늘려 가능한지 확인해본다. 이후 반복..
| 알고리즘 1. window의 시작점과 끝 점을 의미하는 i,j를 0으로 초기화시킨다. 2. basket의 조건에 부합하는 한 계속해서 j를 1씩 증가시킨다. 3. j를 1 증가시켰는데 basket의 조건이 깨진다면 i도 1을 증가시켜서 window자체를 오른쪽으로 1 옮긴 것과 같은 효과를 낸다. 4. 2,3을 반복한다. 5. j가 fruits의 크기에 다다랐을 때의 window 크기가 내가 딸 수 있는 최대 과일의 개수이다. |
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
length = len(fruits);
i = 0; // 시작점
j = 0; // 끝점
basket = {};
while(j < length): // j가 fruits의 길이와 같아질 때까지
if fruits[j] not in basket: // 만약에 basket에 없으면
basket[fruits[j]] = 1; // 넣고
else:
basket[fruits[j]] += 1; // 기존에 있었으면 1을 증가시켜준다.
if len(basket) > 2: // 넣었는데 basket의 조건을 위반하면
if basket[fruits[i]] > 1; // 앞에 있는 원소를 삭제하고 i를 1증가시킨다.
basket[fruits[i]] -= 1;
else:
del basket[fruits[i]];
i += 1;
j += 1; //j를 1 증가시킨다.
ans = j - i; // window의 크기 = 수확할 수 있는 최대 개수
return ans;
Time Complexity: O(N)
밖의 while문을 제외하고는 내부 for문이 존재하지 않기 때문에 시간복잡도는 N이다.
(참고로 dictionary의 key를 통한 탐색은 O(1)이다. == 여기서의 not in 시간복잡도가 1이다.)
Space Complexity: O(1)
basket의 경우 dictionary로 최대 3개의 과일만 들어가기 때문에 O(1)이 된다.
[또다른 방법] ( 가능한 경우의 수를 모두 확인하면서 최대값을 구하는 방법)
| 알고리즘 1. window의 시작점과 끝 점을 의미하는 i,j를 0으로 초기화시킨다. 2. basket의 조건에 부합하는 한 계속해서 j를 1씩 증가시킨다. 3. j를 1 증가시켰는데 basket의 조건이 깨진다면 ans와 현재 window의 크기 중 큰 값을 저장해놓고 i를 basket의 조건이 부합할때까지 증가시킨다. 4. 2,3을 반복한다. |
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
length = len(fruits);
first = 0; end = -1;
ans = 1;
basket = {};
while(end < length):
end += 1;
if end == length:
break;
if fruits[end] not in basket:
basket[fruits[end]] = 1;
else:
basket[fruits[end]] += 1;
if len(basket) > 2:
ans = max(ans, end - first);
if basket[fruits[first]] > 1:
basket[fruits[first]] -= 1;
else:
del basket[fruits[first]];
first += 1;
ans = max(ans, end - first)
return ans;
Time Complexity: O(N)
밖의 while문을 제외하고는 내부 for문이 존재하지 않기 때문에 시간복잡도는 N이다.
(참고로 dictionary의 key를 통한 탐색은 O(1)이다. == 여기서의 not in 시간복잡도가 1이다.)
Space Complexity: O(1)
basket의 경우 dictionary로 최대 3개의 과일만 들어가기 때문에 O(1)이 된다.
문제 링크
https://leetcode.com/problems/fruit-into-baskets/description/
Fruit Into Baskets - LeetCode
Fruit Into Baskets - You are visiting a farm that has a single row of fruit trees arranged from left to right. The trees are represented by an integer array fruits where fruits[i] is the type of fruit the ith tree produces. You want to collect as much frui
leetcode.com
'코테 > LeetCode(Solve)' 카테고리의 다른 글
| [python3] 2306. Naming a Company (0) | 2023.02.09 |
|---|---|
| [python3] 45. Jump Game II (0) | 2023.02.08 |
| [python3] 1470. Shuffle the Array (0) | 2023.02.06 |
| [python3] 1626. Best Team With No Conflicts (0) | 2023.02.03 |
| [python3] 1328. Break a Palindrome (0) | 2022.10.11 |




