| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- python3
- LinkedList
- BFS
- Bellman-Ford
- heap
- stack
- SinglyLinkedList
- ArrayList vs LinkedList
- DailyLeetCoding
- 자료구조
- Union Find
- 광연자동차운전면허학원
- array
- String
- Easy
- leetcode
- greedy
- Leedcode
- VCS
- Two Pointers
- Java
- 구현
- Hashtable
- hash
- sorting
- dfs
- A* Algorithm
- Medium
- graph
- hash table
- Today
- Total
Min IT's Devlog
[python3] 837. New 21 Game 본문
풀이 일자: 23.05.25 ( 나중에 다시 풀어보기..)
난이도: [Medium]
분류: [DP, SlidingWindow, Math]

문제 내용
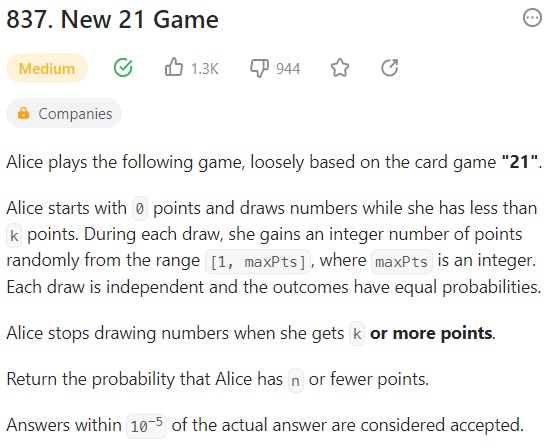
카드가 1부터 maxPts사이의 정수로 이루어져있고 Alice가 초기 점수 0점에서 시작하여 점수의 합이 k이상이 될 때까지 카드를 뽑는다고 한다. 카드 뽑기가 종료되었을 때 Alice의 점수가 n이하일 확률을 구하는 것이 문제이다.
문제 해결 흐름
1. 처음에 해당 문제를 봤을 때 DP라는 것을 바로 알 수 있다.
→ 점수의 합이 k이상이 될 때까지 뽑고 점수가 n이하일 확률이기 때문에 dp배열을 이용하여 점진적으로 확률을 계산하는 수밖에 없다.
여기까지밖에 생각하지 못했다.
다른 해결 방식
1. 처음 문제에서 제공한 알고리즘은 TLE가 발생하지만 간단한 알고리즘을 제시해주었다.(Official Solution)
1) i는 현재 Alice의 point이고 j는 현재 i를 만들기 위해 이전 시점에 뽑은 카드의 번호라고 생각하면 된다.
2) 이 경우 당연히 j는 i를 넘을 수 없고 i와 j의 차가 k는 될 수 없다.
3) 가능한 모든 경우의 확률을 모두 i에 더하는 방법이다.
class Solution:
# 매우 간단한 알고리즘이지만 TLE 발생
def new21Game(self, n: int, k: int, maxPts: int) -> float:
dp = [0] * (n + 1) # dp를 위한 arr 생성
dp[0] = 1 # Alice가 0points를 가지고 있기에 dp[0]= 1;
for i in range(1, n + 1): # 1부터 n points까지 순회
for j in range(1, maxPts + 1): # 다음에 뽑는 j는 1부터 maxPts로 정함
if i - j >= 0 and i - j < k: # i는 j보다는 크거나 같아야 한다고 가정했음. 현재 뽑는게 끝이 아니기 위해 k보다는 작야야해.
dp[i] += dp[i - j] / maxPts # 현재 i points를 같기 위해서는 이전의 확률에 maxPts를 나눈 만큼의 결과가 나옴.
return sum(dp[k:]) # 각 k이상이 나올 확률을 모두 더해서 리턴한 것.=> 매우 직관적인 알고리즘이었지만 시간적으로 n과 maxPoint가 비슷하다는 가정하에 N^2의 시간복잡도를 가진다.
Time Complexity: O(N^2)
최악의 시간복잡도는 n과 maxPoint가 비슷해지는 경우로 N^2의 시간복잡도를 가진다.
Space Complexity: O(N)
확률을 저장할 배열을 사용했기 때문에 N의 공간복잡도를 가진다.
2. 이후 최적화된 방식을 소개해주고 있는데 잘 이해가 되지 않는다.ㅎ(Official Solution)
class Solution:
def new21Game(self, n: int, k: int, maxPts: int) -> float:
dp = [0] * (n + 1)
dp[0] = 1
s = 1 if k > 0 else 0
for i in range(1, n + 1): # 1~n사이의 points
dp[i] = s / maxPts # i가 될 확률
if i < k: # n < k이면
s += dp[i] # s에 dp[i]를 더함
if i - maxPts >= 0 and i - maxPts < k: # maxPts <= n < maxPts + k이면 sliding window의 첫번째를 뺌.
s -= dp[i - maxPts] # s -= dp[n-maxPts]
return sum(dp[k:]) # k부터 n까지의 확률을 모두 더함.
이해한 대로 생각을 해보면
sliding window를 늘려가면서 s의 확률을 계속해서 더하고 sliding window의 크기가 maxPts가 되면 앞의 확률은 빼고 뒤의 확률를 더하는 전형적인 sliding window 방식인데 s를 통한 확률 계산 부분이 잘 이해가 가지 않는다.
Time Complexity: O(N)
시간복잡도는 sliding window를 사용함으로써 내부 for문을 사용하지 않고 이에 N의 시간복잡도를 가지게 된다.
Space Complexity: O(N)
확률을 저장할 배열을 사용했기 때문에 N의 공간복잡도를 가진다.
문제 링크
https://leetcode.com/problems/new-21-game/description/
New 21 Game - LeetCode
Can you solve this real interview question? New 21 Game - Alice plays the following game, loosely based on the card game "21". Alice starts with 0 points and draws numbers while she has less than k points. During each draw, she gains an integer number of p
leetcode.com
'코테 > LeetCode(Unsolved)' 카테고리의 다른 글
| [python3] 1514. Path with Maximum Probability (1) | 2023.06.28 |
|---|

